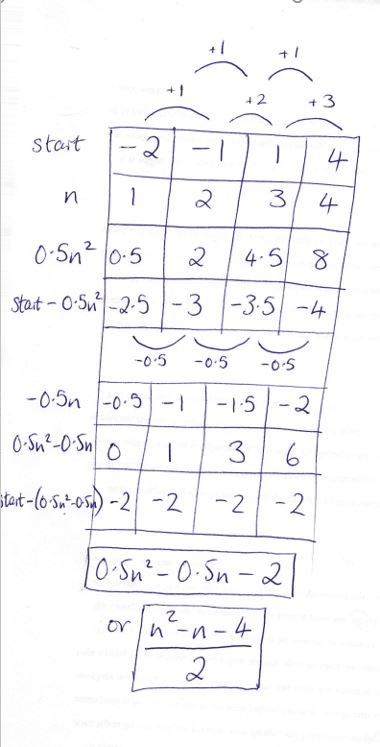
Intro here.
These are the notes (and some cat pictures) from the first iteration of this talk, which I’ve now delivered in a few places. There’s a recording of the talk here. You can see details of when I have delivered / will deliver it here.

Making people feel stupid: What does it mean?
- People listen to what others say.
- They overhear them judging people for not being clever enough or not knowing enough.
- They internalise it. They worry that they will be next.
What’s wrong with me?
- Maybe you’re quietly judging me already. Maybe you’re thinking, she’s probably not very clever and doesn’t like it when she gets exposed.
- Maybe you’re right! I often think that about myself. But I have a maths degree, 18 years experience, I’m a tech lead with a major international consultancy, etc.
- So, that was me imagining that you might judge me for being stupid. Maybe you did and maybe you didn’t. But the point is, I imagined that you would. Because I’m so used to people in tech judging each other for being stupid.
My story
- I’ve always felt there was something wrong with me because I struggle to understand things unless they’re explained in simple concrete terms.
- And yet I can do complexity.
- I can build complex systems out of simple parts.
- If anything, my flaw is a tendency towards too much complexity.
- …which is why I deliberately break things down into simple parts.
- …but I also forget complex terminology – I recall easier-to-remember equivalents instead.
- I have missed out on jobs because people were bemused by my apparent lack of expertise.
- I have been told in interviews that I wasn’t competent because I couldn’t respond to the kind of question that requires you to have memorised stuff.
The Impact:
Impact on the industry
- Facts, Figures, Statistics:
- There will be an estimated 1 million more computing jobs than applicants who can fill them by 2020. This figure was projected by Code.org, based on estimates from the U.S. Bureau of Labor Statistics on job creation and separately, estimates of college graduation rates by the National Science Foundation.
- Only 11% of employers (US) believe higher education is “very effective” in readying graduates to meet skills needed in their organisations.
- Some 62% (US) said students were unprepared.
- US: There are more than 500,000 open computing jobs nationwide, but less than 43,000 computer science students graduated into the workforce in 2016.
- In 2016, the White House claimed the federal government alone needed an additional 10,000 IT and cybersecurity professionals.
- Source, March 28th 2017: https://www.usatoday.com/story/tech/talkingtech/2017/03/28/tech-skills-gap-huge-graduates-survey-says/99587888/
Impostor syndrome
- Hands up if you feel like other people are cleverer / doing things better than you?
- Impostor syndrome: “Somehow everybody has failed to notice how rubbish I am.”
- I hate – am almost incapable of – playing the game where everything is obfuscated and translated into a language that only the elite can understand.
- Ironically this means that my impostor syndrome is at least partially based around the fact that I don’t seem capable of doing the things that entrench everybody else’s impostor syndrome.
- I can hit the ground running, but I keep forgetting.
- I have to prove it to myself over and over again.
Scenario A: Meeting where people talk jargon & nobody understands
- Me: Hi, sorry I’m late.
- Them: It’s fine, we were just talking about the ARM processor.
- Me: Ah right, yes of course.
- Shit, ARM, I know I’ve heard of that before. ARM, um…
- [some stuff I don’t hear cos I’m trying to remember what ARM stands for]
- Me: “Look folks, I’m so sorry, but I’ve forgotten what ARM stands for?”
- Them: “Articulated retention matriculation.”
- Me: I have NO idea what that is. I’ll work it out as I go along.
- Somebody else: Actually guys, I think we should be considering AMRM at this point.
- Me: AMRM?
- Reply: Articulated meta-retention matriculation.
- [someone else, not me]
- That’s a very good point! We definitely need to get meta at this juncture.
- Oh God, I was only just following this, but now they’ve lost me. Meta? What does meta mean in this context? What does meta mean in any context? It’s one of those terms that always confuses me, I know that much.
- Oh well, I said juncture. I love saying juncture. It’s the perfect word for situations like this.
- [some stuff that Person2 misses cos they’re worrying about what meta means]
- Etc
Diversity and Inclusion
- People want to fit in.
- Two effects:
- They use jargon to create a shared identity.
- They feel bad if they feel like an outsider.
- People will leave, or not join in the first place, because they feel excluded.
- This disproportionately affects under-represented groups.
- Stereotype threat: https://en.wikipedia.org/wiki/Stereotype_threat
- “…men in STEM subject areas overestimate their own intelligence and credentials, underestimate the abilities of female colleagues, and that as a result, women themselves doubt their abilities — even when evidence says otherwise.”
- Stereotype threat has been shown to reduce the performance of individuals who belong to negatively stereotyped groups.
- If negative stereotypes are present regarding a specific group, group members are likely to become anxious about their performance, which may hinder their ability to perform at their maximum level. Importantly, the individual does not need to subscribe to the stereotype for it to be activated.
- It is hypothesised that the mechanism through which anxiety (induced by the activation of the stereotype) decreases performance is by depleting working memory (especially the phonological aspects of the working memory system).
- Two effects:
Talking in jargon
- These insecurities cause people to increase the amount of jargon they use.
- They want to prove how clever they are.
- Their colleagues struggle to understand them, but they pretend they do, to avoid looking stupid…
- Complex impenetrable language is what people deploy as a kind of force field
- Weird vicious cycle: everybody obfuscates to protect themselves from potential exposure as somebody who doesn’t fully understand.
- In the process they confuse everybody around them, who in turn become terrified that somebody is going to notice that they don’t fully understand what’s going on, so they join in the game, make everything they say sound complicated, and so the cycle continues.
- There does come a point where you’ve been immersed in it for long enough that only some of it is confusing, and some/most of it makes sense.
- That’s quite a kick!
- You have to pay your dues to get to that point, and it feels good. You feel special.
- So you pull the ladder up behind you.
- You had to go up it, and so should everybody else.
- You’re in the club now, and you want to savour that.
- So you join with your new comrades in mocking those who still haven’t arrived.
- You make no concessions in your language.
- You’ve learnt what it means! It was hard! Why would you waste all that hard work and abandon your hard-won vocabulary by explaining things in simple terms?
- Explaining things in simple terms takes twice as long anyway.
- Giving the answer you think people want to hear:
- The hairdresser asked me whether I had straighteners and I answered Yes. Why? Because I felt like it was the “right answer”. I don’t have straighteners. I’m never going to manage this labour-intensive haircut I’ve been given.
Scenario E: When talking jargon feels good
- I felt all pleased with myself recently when I worked out how to join in with a hangouts conversation by using words like “discoverability” and “distinguishable”. I felt less insecure, and like I was now a proper grownup, a member of the club. But meanwhile there may well be somebody somewhere hearing nothing but “blah blah blah”…
Reasonable reasons
- Is it sometimes ok?
- “I can’t spend my whole time teaching people, I need people who can hit the ground running.”
Unreasonable reasons
- Many people project a sheen of knowledge.
- Many limit themselves by seeking to preserve knowledge once they find it.
- People focus on their own experience – making themselves look good.
- But when they look at someone else, they have a different agenda.
- They don’t stop to wonder whether they have ever said anything “stupid” like that themselves – and if they did, WHY?
- Or they remember it full well and don’t want anyone else to remember, so distract attention by joining in with the attackers.
- We identify the things we CAN remember, then we fetishise them.
- We push them over alternatives.
- Not necessarily because they are better – just because we feel more comfortable there.
Definition of competent
- What really impacts on you and your team?
- Is it lack of knowledge?
- What does it actually take to be good at your job?
- What is the definition of competent?
- What is the definition of intelligent?
- “Be curious. Read widely. Try new things. What people call intelligence just boils down to curiosity.” – Aaron Schwartz.
People who are not techies are impacted too
- Examples of support staff, stakeholders, non-technical people… being made to feel stupid.
My personal experience – the happy story
- How I learnt to attack new knowledge outside my comfort zone.
- The irony is that my career – and my enjoyment of it – has improved dramatically since I started admitting ignorance.
Why Empathy is so Important
- “They only care about making themselves look good.”
- This in itself is judgmental.
- Think about how it feels like to be them!
- You can find yourself alienating others without ever having conscious malicious intentions.
- Other people know other stuff.
- Two effects:
- One: When they know stuff you don’t, you feel insecure.
- Two: When you know stuff they don’t, you can get impatient.
- Two effects:
Conclusions / Advice
- Maybe you see me as an idealist. Or maybe I’m a pragmatist. Over the years I’ve paid attention to what works in life and what doesn’t. What makes people ill, what doesn’t. These are all practical hints for survival.
- Does it actually matter how much people know? Industry constantly moving, people forget stuff.
- Some of the most important moments in my career have been the times I’ve realised that my colleagues are also confused.
- Eternal thanks to those that admitted it.
- People are often scared to admit confusion.
- I often don’t know what I’m doing.
- The range of knowledge in our industry is VERY WIDE.
- Don’t expect other people to know what you know, and vice versa.
- People forget things they once knew.
- If people don’t know enough, WHY is that? What’s deterring them?
- What would happen if we changed the rules?
-
- Focus on aptitude – recruitment becomes easier.
- Encourage people to explore and experiment and learn WITHOUT RISK.
- Stops people pushing less optimal solutions.
- Make explicit statements to newcomers to your team, at start of meetings, etc – have a policy towards curiosity – keep repeating that simple questions are ok, that mistakes are ok, that if somebody doesn’t know something it’s in the interests of the whole team to help them learn. Plus, active encouragement to give feedback if these aims are not being met.
- Tweet from Tim Post (@TinkerTim) re Stack Overflow:
- “You can’t work on problems that you’re unwilling to admit. Wanting help often means being vulnerable enough to ask for it, and that’s where we are. Let’s keep making the internet better, without hurting people in the process.”
- WE SHOULD ALL ENCOURAGE PEOPLE TO ASK QUESTIONS.
The Stupid Manifesto
LET’S STOP MAKING EACH OTHER FEEL STUPID. INSTEAD, LET’S…
- Have an explicit policy of curiosity towards all things
- Encourage each other to shout out if we discourage curiosity
- Ask what people NEED to know, not what they know
- Never judge someone because their knowledge doesn’t match ours
- Give our colleagues every opportunity to learn and explore WITHOUT RISK
- Give new people a chance to show us what they can do
- ENCOURAGE EVERYONE TO ASK QUESTIONS
- Acknowledge the broad range of knowledge in our industry
- Remember our industry never stays the same
- Remember we all forget stuff
- Lead by example: Be honest when we’re confused
- Focus on aptitude, not knowledge
- Remember what it feels like when we are still learning
- Prioritise clarity over jargon
- Remember this is not idealism, it’s pragmatism
- LET’S STOP MAKING EACH OTHER FEEL STUPID.
Useful resources and references:
- Stereotype threat: https://en.wikipedia.org/wiki/Stereotype_threat
- Delusions of Gender: Cordelia Fine
- April Wensel (@aprilwensel): Compassionate coding
- Blog: https://medium.com/compassionate-coding
- Site: https://compassionatecoding.com/
- “Software development that values humans”
- https://insimpleterms.blog/2017/10/16/advice-for-women-or-anyone-starting-a-career-in-tech/ – Advice for anyone starting a career in tech
- https://insimpleterms.blog/2017/10/13/resources-for-women-arriving-at-or-returning-to-it/ – Resources for Women Arriving at or Returning to IT
- https://insimpleterms.blog/
- https://medium.com/a-woman-in-technology – learning, teaching, women in tech, maths
-