I was in a workshop the other day and I started a doodle which I often do (or some version of it) when I’m in meetings and such:


I Iove drawing pentagrams because they’re so satisfying – five quick lines is all you need, without lifting your pen from the paper.
But whenever I do this doodle, it always bothers me that these are not really pentagrams, and the contained shapes are not pentagons. I often wonder what would happen to the tesselation if I was drawing real pentagons. I also wonder how I could draw proper pentagrams without a protractor.
(For clarity, a pentagram is a five-pointed star. A pentagon is a five-sided shape. And when I say “real” I mean “regular” – ie shapes with rotational symmetry, where every point, every angle, every side is equal. And “tesselation” is a word that describes the way different shapes slot together side by side, with no gaps (I learnt that word in primary school, in relation to Roman mozaics):
 ).
).
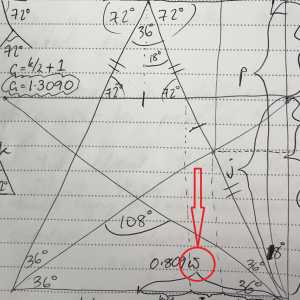
So during this workshop I did some trigonometry to work it all out. For those of you who were there with me, this is what I was scribbling in the breaks when I was being so antisocial:
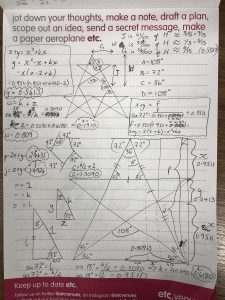
The conclusion I came to was that on lined paper, I could get a reasonable approximation of a pentagram using the following proportions:


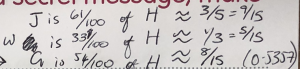
If you’re wondering what w represents, I drew it on a different diagram when I realised that G and w were not the same distance – they only appeared to be because I was drawing non-regular pentagrams:
Based on these proportions and the dots that each horizontal line was made of, I came up with the following not-bad pentagrams (they’d probably be better if I had a ruler available instead of drawing freehand):

…and now the pentagons are all regular pentagons, and the pentagrams are regular too, but they’re forced to collide with each other as a result.
For the sake of aesthetics I think I prefer the non-regular versions at the top of this post, but the mathematician in me is now happy. 🙂

Hey. LOVED YOUR POST!!! I’m super excited. Just started studying pentagrams and such however, (not trying to be funny) … Perhaps you should consider grammatically moving tessellation behind its introduction. Makes the pieces flow with an impeccable feng shui. TRUST! Thanks for this information. It takes 1!
Thank you aja!
I’m not actually sure what you mean by “grammatically move tesselation behind its introduction” though. Can you clarify please?